6.5 Two dimensional parabolic PDE:
The error analysis and stability theory developed for one dimensional diffusion problems can be extented to two-dimensional diffusion equations. Consider the two dimensional heat equation in the unit square
................. (6.4.31)
subject to some known initial conditions.
................. (6.4.32)
and boundary conditions
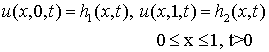
................. (6.4.33)
By superimposing an uniform mesh of step lengths 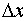 and
and 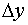 respectively in space directions x and y on the unit square at time t = 0, coordinates of any typical node P(xi, yj) can be obtained by the relations
respectively in space directions x and y on the unit square at time t = 0, coordinates of any typical node P(xi, yj) can be obtained by the relations
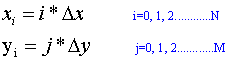
................. (6.4.34)
(for unit square the number of nodal points in x and y directions can be equal that is, N = M, then 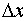 =
=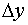 ).
).
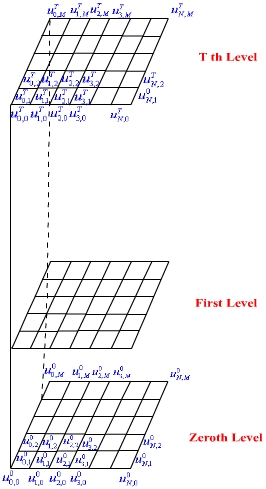
Figure 6.4.4 Representation of 2D Grid
By taking a similar mesh at various t > 0 (with 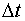 as step length) as shown in figure 6.4.4, the coordinates of any space node P(xi, yi, tn) can now be obtained by adding
as step length) as shown in figure 6.4.4, the coordinates of any space node P(xi, yi, tn) can now be obtained by adding
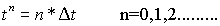
.................(6.4.35)
to (6.4.34). Since the solution 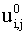 at t=0 is known from the initial conditions, the solution at the time level n=1 is obtained by various schemes after making use of boundary conditions. This process is repeated until the requtred time level is reached.
at t=0 is known from the initial conditions, the solution at the time level n=1 is obtained by various schemes after making use of boundary conditions. This process is repeated until the requtred time level is reached.
FTCS Scheme:
By using forward difference to time derivative and central differences to space derivatives in (6.4.31) we get
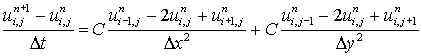
for i = 1, 2, 3 . . . N-1, j = 1, 2, 3 . . . M-1 and n = 0, 1, 2 . . .
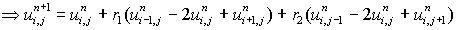
.................(6.4.36)
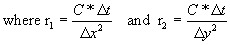
for i = 1, 2, 3 . . . N-1, j = 1, 2, 3 . . . M-1 and n = 0, 1, 2 . . .
Since (6.4.36) has only known values on the right hand side the only unknown in the equation is 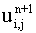 , so the scheme is explicit and
, so the scheme is explicit and 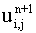 is obtained at (xi, yj, tn+1) by simple substitution.
By repeating the same for i = 1, 2, 3 . . . N-1 and j = 1, 2, 3 . . . M-1 , the solution to 2D heat equation (6.4.36) at time t=(n+1) *
is obtained at (xi, yj, tn+1) by simple substitution.
By repeating the same for i = 1, 2, 3 . . . N-1 and j = 1, 2, 3 . . . M-1 , the solution to 2D heat equation (6.4.36) at time t=(n+1) * 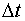 is obtained. This process is repeated until the final time level has been reached.
is obtained. This process is repeated until the final time level has been reached.
Truncation error of 2D - FTCS Scheme:
From (6.4.36) we have
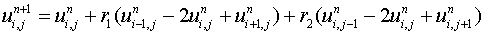
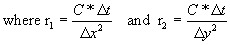
By Taylor series expansions:
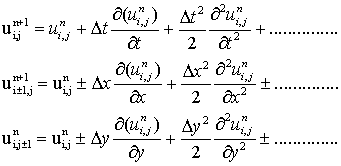
.................(6.4.37)
Subsituting (6.4.37) in (6.4.36) gives
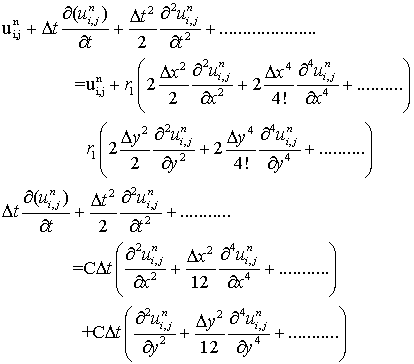
Divide with 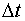 and then using (6.4.31) gives,
and then using (6.4.31) gives,
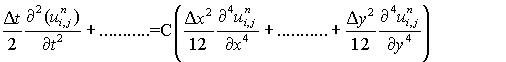
that is, the truncation error is
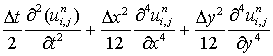
.................(6.4.38)
ane the order of the scheme is 1, 2 and 2 respectively in t, x and y directions.