Truncation error and order of the schemes:
The truncation error defined for ordinary differential equations is also can be extended to partial differential equations. In ODE, since there is only one independent variable, all the dependent variables in the corresponding finite difference equation, are
expanded at the node xi using Taylor series expansion and the first non-zero term of the resultant infinite series is called the truncation error of the scheme and the power of the steplength term(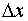
) in this truncation error term is called the order of the scheme. In partial differential equations since there are more than one independent variable, the finite difference equation at any typical node say (xi, tn) is expanded at (xi, tn) in terms of Taylor series and then the order of the scheme is nothing but the powers of the step length terms 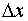and 
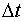. For example, for any scheme, the infinite series obtained after expanding the terms the difference equation using Taylor series is
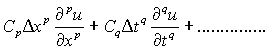
Then the scheme is called of pth order in x, qth order in t and the truncation error is
.................
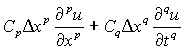(6.4.11)
