Stability of the numerical schemes
In application of any numerical scheme to solve a differential equation, if small change in the input data leads to only a small change in the output data then such a numerical scheme is called stable. Since numerical solutions obtained using computer are proned to round off errors, unless the numerical scheme under use is stable, these errors will get magnified during the iterative process and even dominate the solution.
There are two different approaches to study the stability of the numerical schemes. In the first method, the difference equations are expressed in matrix form and the eigen values of the associated matrix are examined. In the other, finite fourier series is used to analyze the stability. The later method is much simpler to use than the former however, the later method is less rigorous because it neglects the boundary conditions.
Matrix method of Stability of FTCS scheme:
Consider the explicit FTCS scheme (6.4.2) to one dimensional diffusion
equation;
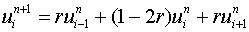
for i = 1, 2, 3 . . . N-1 and n = 0, 1, 2 . . .
with boundary conditions u = 0 at x = 0 and 1 for all t greater than zero and with some known initial values of u at t=0.
The system of equations (6.4.2) for a particular time level say 'n', in matrix form can be written as
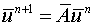
................. (6.4.15)
where
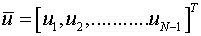
and 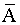 is the (N-1)*(N-1) triangular matrix of the form
is the (N-1)*(N-1) triangular matrix of the form

Equation (6.4.15), can be rewriten as
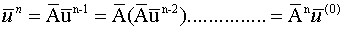
................. (6.4.16)
where the vector 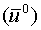 is u with some known initial values at time t=0.
is u with some known initial values at time t=0.
Since any numerical solution is bound to rounding errrors, let us assume that at time t=0 computations are started with 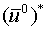 instead of
instead of 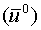 . That is,
. That is,
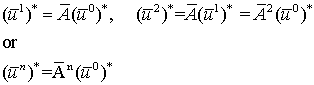
So that, the total error at n th time level 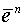 is
is
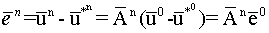
................. (6.4.17)
Equation (6.4.17) is similar to (6.4.16) except e in the place of u shows that the formula for the propagation of the error is same as that for the solution of u.
Assume that the matrix 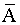 is non-deficient, that is, it has (N-1) linearly independent eigen vectors
is non-deficient, that is, it has (N-1) linearly independent eigen vectors 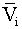 (which is always the case if
(which is always the case if 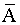 has distinct eigen values li or the coefficient matrix
has distinct eigen values li or the coefficient matrix 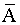 is real and symmetric). Then these (N-1) linearly independent eigen vectors can form a basis for the (N-1) dimensional space in which
is real and symmetric). Then these (N-1) linearly independent eigen vectors can form a basis for the (N-1) dimensional space in which 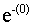 is one of the elements. Hence,
is one of the elements. Hence,
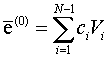
................. (6.4.18)
where ci, i = 1, 2, 3 . . . N-1 are some known constants.
Now consider the equation (6.4.17) to find the error at the n th time level
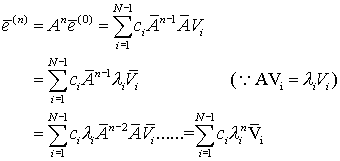
................. (6.4.19)
This error has to be bounded as the number of iterations 'n' increases infinitely, that is 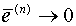 as n--->0. From equation (6.4.19) this condition is satisfied whenever maximum of |li| < 1 that is the maximum of the absolute value of the eigen values of
as n--->0. From equation (6.4.19) this condition is satisfied whenever maximum of |li| < 1 that is the maximum of the absolute value of the eigen values of 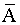 is less than one. So to check for the stability of any numerical scheme it is sufficient to check for the modulus of the largest eigen value of the coefficient matrix
is less than one. So to check for the stability of any numerical scheme it is sufficient to check for the modulus of the largest eigen value of the coefficient matrix 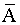 is to be less than unity.
is to be less than unity.
For FTCS scheme the coefficient matrix 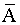 is
is
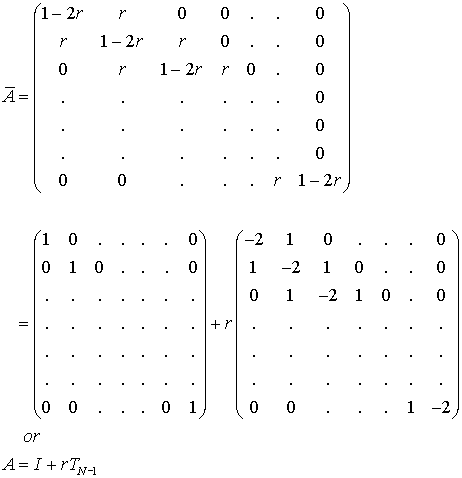
................. (6.4.20)
where I is the identity matrix of order (N-1)*(N-1) and TN-1 is a square matrix of order (N-1) with eigen values
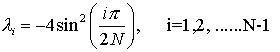
................. (6.4.21)
and the corresponding eigen vectors are
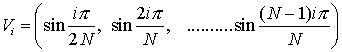
................. (6.4.22)
From (6.4.20) and (6.4.21) the eigen values of 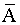 are
are
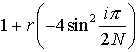
................. (6.4.23)
Hence the condition for stability is
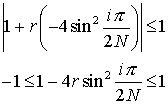
Since 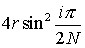 is always positive, the only useful condition is
is always positive, the only useful condition is
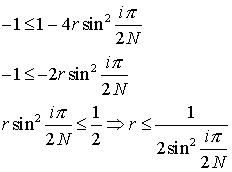
................. (6.4.24)
Conditon (6.4.24) is always true whenever 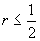 that is, the condition for FTCS scheme is to be stable is r must be less or equal to 1/2. This is precisely what has been observed in the example 6.4.1. For this problem if FTCS scheme with r > .5 is used, to obtain the numerical solution the solution became unphysical.
that is, the condition for FTCS scheme is to be stable is r must be less or equal to 1/2. This is precisely what has been observed in the example 6.4.1. For this problem if FTCS scheme with r > .5 is used, to obtain the numerical solution the solution became unphysical.
Stability of the Crank-Nicolson scheme:
Consider the Crank-Nicolson scheme to the one-dimensional diffusion equation with zero boundary conditions and some known initial conditions(6.4.7)
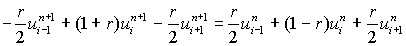
for i = 1, 2,.......N-1 and r = 0, 1, 2.................

Therefore the iterative matrix for the present scheme is
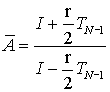
and the eigen values of this matrix are
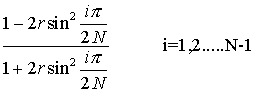
................. (6.4.25)
In(6.4.25) for all positive values of r the denominator is greater than the numerator makes modulus of eigen values of 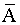 less than one. Hence Crank-Nicolson scheme is unconditionally stable. This is again reflected in the example 6.4.2 because the scheme was giving reasonable
results even with r=1.
less than one. Hence Crank-Nicolson scheme is unconditionally stable. This is again reflected in the example 6.4.2 because the scheme was giving reasonable
results even with r=1.