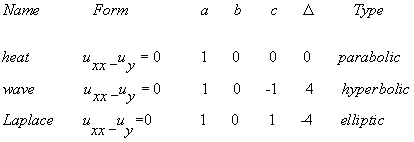Quasi-Linear Second-Order Equations: Characteristics
In this section, we consider the quasi-linear second order partial differential equation of the form
.................
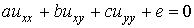
(6.6.11)
where a, b, c and e
are functions of x, y, u, ux and uy.
As in our study of characteristic curves for first-order equations, here also we examine the behaviour of the solution function along a curve in the xy-plane.
Characteristic Curves
Let C be a curve in the xy-plane given parametrically
by
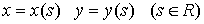
Let us use the traditional notation p=ux and q=uy
and x, y p, q, u indirectly as functions
of s. By direct differentiation, we have
.................
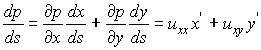
(6.6.12)
.................
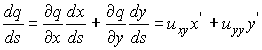
(6.6.13)
Solving (6.6.12), for uxx
gives
.................
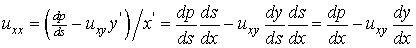
(6.6.14)
Similarly (6.6.13), gives
.................
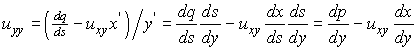
(6.6.15)
These equations, (6.6.14) and (6.6.15) are valid along the curve
C. If the expressions just derived are substituted in Equation
(6.6.11), the result is
.................
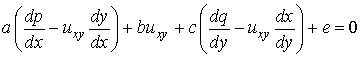
(6.6.16)
Multiply with dy/dx, we get
.................
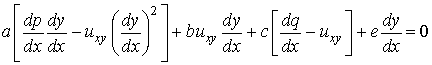
(6.6.17)
Rearranging the equation by colletive the terms uxy, we get
.................
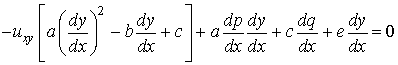
(6.6.18)
The curve C, unspecified until now, is to be chosen such that the coefficient of uxy becomes zero in (6.6.18). Thus, C is described
by the differential equation
.................
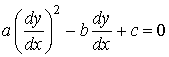
(6.6.19)
Such a curve C is called a characteristic curve
of the differential Equation(6.6.11).
Classification
Since (6.6.19) is a quadratic equation in dy/dx, the nature of
the characteristic curves is determined by the discriminant.
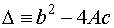
If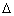 
> 0 at a certain value (x, y, u), then the differential
equation is said to be hyberbolic there. If <
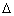0, it is called elliptic. This classification can vary from point to point in
the xy-plane, and it can depend also on the solution u, since
a,b, and c depend only on x and y, and the classification
becomes simpler.
This classification of equations is nicely illustrated by three
faniliar equations that are prototypical:
