Example 6.4.2:

Solve the problem given in example 6.4.1 using Crank-Nicolson scheme .

The Crank-Nicolson scheme (6.4.7) is

for i = 1, 2, 3.........N-1 and n = 0, 1, 2, 3.....................

 

or in the matrix form AU = B where B is the right side known vector.

 

x=	0	.1	.2	.3	.4	.5
n=0	0	.09	.16	.21	.24	.25
n=1	0	.088091	.158004	.208	.238	.248
n=2	0	.086349	.156023	.206	.236	.246
n=3	0	.084744	.154069	.204005	.234	.244
……	……	……	……	……	……	……
n=10	0	.075960	.141451	.190195	.220053	.230016
……	……	……	……	……	……	……
n=20	0	.067068	.126424	.172145	.200671	.210334
……	……	……	……	……	……	……
n=49	0	.049486	.099030	.0129254	.151788	.59536

Table 6.4.5

 

x=	0	.1	.2	.3	.4	.5
n=0	0	.09	.16	.21	.24	.25
n=1	0	.081716	.150294	.200051	.23	.24
n=2	0	.075858	.141421	.190316	.220069	.230027
n=3	0	.071109	.133518	.180934	.210264	.220120
……	……	……	……	……	……	……
n=10	0	.048983	.093086	.127977	.150308	.157987
……	……	……	……	……	……	……
n=20	0	.029952	.056971	.078412	.092176	.096919
……	……	……	……	……	……	……
n=49	0	.007242	.013775	.018960	.022289	.023436

Table 6.4.6

 

 

x=	0	.1	.2	.3	.4	.5
n=0	0	.09	.16	.21	.24	.25
n=1	0	.075359	.141436	.190387	.220110	.230055
n=2	0	.066908	.126194	.172122	.200748	.230429
n=3	0	.059972	.113696	.155782	.182488	.193615
……	……	……	……	……	……	……
n=10	0	.029934	.056937	.078366	.092123	.096863
……	……	……	……	……	……	……
n=20	0	.011238	.021376	.029422	.034587	.036367
……	……	……	……	……	……	……
n=49	0	.000656	.001248	.001717	.002019	.002123

Table 6.4.7

 

Tables 6.4.5, 6.4.6 and 6.4.7 are the numerical solutions respectively with r=0.1, 0.5 and 1.0. Unlike FTCS scheme the solution doesn't oscillate even with r=1. The solutions with r=1 at various t and x is compared in the table 6.4.8 with analytical solution. It is very clear from this table that the numerical and analytical solutions are in good agreement. However the only disadvantage with Crank-Nicolson scheme over FTCS scheme is the computational effort involved at each time level which is relatively high.

 

Weighted average scheme

The weighted average of schemes(6.4.2) and (6.4.5) given by

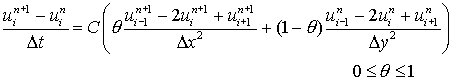
                                                                                                                       ................. (6.4.8)

for i = 1, 2, ..............N-1 and n = 0, 1,2, 3.............

is called the weighted average scheme for one dimensional heat equation. Here, q =0, 1/2 and 1 gives FTCS, Crank - Nicolson and fully implicit schemes respectively.

Three level schemes

All the schemes discussed until now are two level since only two time levels that is n^th and (n+1)^th are involed. If we use central differences to approximate both time and space derivative terms we get

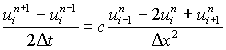
                                                                                                                       ................. (6.4.9)

for i = 1, 2, 3 ...........N-1 and n = 1, 2............

For n = 1 the scheme needs the solution at 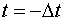level which is outside the domain of interest and we may not have any information about u at this time level. Hence at n=1 it is necessary to use a different scheme and from n = 2 onwards the schems(6.4.9) can be used. If we replace 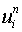term in (6.4.9) with

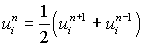
Then we get

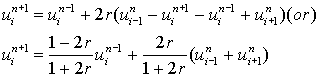
                                                                                                                     ................. (6.4.10)

This difference scheme is called Dufort and Frankel explicit method.