Method of solution for Neumann Problem:
If the boundary condition(s) on one or more boundaries have any derivative terms, say,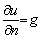 
on some boundary (n is normal direction and g is some known function) then the differential equation (6.5.6) along with the boundary conditions is called Neumann problem. Since u is also an unknown on the boundaries where the derivative boundary conditions are given, the approximation of the differential equation to difference equation at the nodal points inside the domain of interest does not result an equal number of equations compared to the number of unknowns.
The required extra equations have to be generated by using finite difference approximations of the boundary conditions at the nodal points of the boundaries.
For example if y = k (some constant) is the boundary
where a derivative boundary condition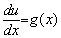 
is given then 
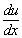is approximated either with 
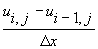or with 
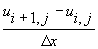depending upon whether 
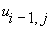or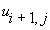 
is inside the domain of interest.
since forward or backward differences are used to approximate the derivative boundary conditions, the order of approximation is only one. To increase the order of approximation, there is another practice of approximating the given differential equation on the boundaries where Naumann type of conditions are given, with central differences. This result in a system with extra nodes lying outside the domain of interest. These extra unknowns now can be eliminated by writing them in terms of the function values inside and on the boundary nodes where the derivative boundary conditions are given by approximating the derivtive boundary condition with central differences. This process raises the order of approximation to two, however this method violates the condition that the differential equation may not valid on the boundaries.
Example 6.5.2:
Consider the Poisson's equations
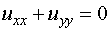
in the unit square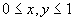 
with Dirichlet boundary conditions u(x,y)=0 on boundaries x=0, x=1 and y=0. And the Neumann boundary condition 
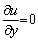at y=1. Solve for u in 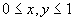using finite difference method with step length 0.25 in both x and y directions.
Solution:
The computational mesh and the approximation of the given PDE at the nodes i = 1, 2, 3 and j = 1, 2, 3 is similar to the corresponding mesh and finite difference system given in problem 6.5.1. Hence the resultant algebriac system is (from 6.5.11)
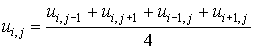
for i = 1, 2, 3 and j = 1, 2, 3
................. (6.5.12)
Also from the Neumann condition at y=1 we have
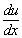= 0 that is at j = 4.
By making use of backward difference at y = 1 (at j = 4) we get
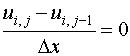
at i = 1, 2, 3 and j = 4
that is
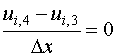
for i = 1, 2, 3
or
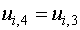
for i = 1, 2 and 3 . . . (6.5.13)
The two sets of equations (6.5.12) and (6.5.13) give twelve equations to solve the twelve unknowns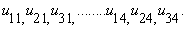 
If we solve this system with Gauss-Elimination or with any iterative method the solution comes as
